活用定义简化过程提高运算能力

活用定义简化过程提高运算能力

张艳春

山西省忻州市第一中学 034000

摘要：求解解析几何问题中，求轨迹问题，解决圆锥曲线几何量问题，求最值问题，活用定义进行化归与转化，都能使运算过程简捷，运算结果准确，提高运算能力。

关键词：解析几何中的运算，活用定义，简化过程，提高运算能力

数学定义本身在解题中有着广泛的应用,提高对定义运用的灵活性,有时将大大简化某些问题的求解过程,起到事半功倍之效。求解解析几何问题中活用圆锥曲线定义，能做到过程简单，结果准确，提高高中学生运算能力。

一、利用定义求轨迹问题

若动点的运动规律符合某圆锥曲线的定义,可以先判断其轨迹,再求出轨迹方程.过程简捷，结果准确，提高了学生运算能力。

【例1】已知两个定圆O₁和O₂，它们的半径分别为1和2，且|O₁O₂|＝4，动圆M与圆O₁内切，又与圆O₂外切，建立适当的坐标系，试求动圆心M的轨迹方程。

【解析】以两个定圆圆心O₁和O₂所在的直线为x轴，线段O₁O₂的垂直平分线为y轴,建立平面直角坐标系，设动圆心M（x，y）,半径为R. 则O₁(-2,0)，O₂（2,0）

依题意：|MO₁|=R-1,|MO₂|=R+2,∴|MO₂|-|MO₁|=3<|O₁O₂|＝4，所以M点的轨迹是以O₁(-2,0)，O₂（2,0）为焦点，实轴长为2a=3的双曲线的左支.即a=,c=2, b²= c²- a²=.所求轨迹方程为-＝1（x≤-）.

【评析】活用双曲线定义，先判断轨迹类型，进而求轨迹方程运算简捷，结果准确。

【针对练习1】

如图, 在△ABC中,已知|AB|=4Error: Reference source not found,且三个内角A,B,C满足2sinA+sinC=2sinB,建立适当的坐标系,求顶点C的轨迹方程.

【解析】以AB边所在的直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系如图所示,则A(-2Error: Reference source not found,0),B(2Error: Reference source not found,0).由正弦定理得sinA=Error: Reference source not found,sinB=Error: Reference source not found,sinC=Error: Reference source not found(R为△ABC的外接圆半径).

因为2sinA+sinC=2sinB,所以2a+c=2b,即b-a=Error: Reference source not found从而有|CA|-|CB|=|AB|=2Error: Reference source not foundError: Reference source not found<|AB|.由双曲线的定义知,

点C的轨迹为双曲线的右支(除去与x轴的交点). 因为a=Error: Reference source not found,c=2Error: Reference source not found,所以b²=c²-a²=6,

即所求轨迹方程为－=1 (x>Error: Reference source not found).

【评析】用正弦定理将角的问题转化为长度问题，用双曲线定义，先判断轨迹，建立适当坐标系，最后写出方程。

二、利用定义求解圆锥曲线几何量问题

圆锥曲线中涉及焦半径、焦点三角形周长、面积，离心率等问题，充分利用圆锥曲线定义解题，过程简捷，结果准确。提高了学生运算能力。

【例2】如图所示,已知椭圆的方程为＋＝1，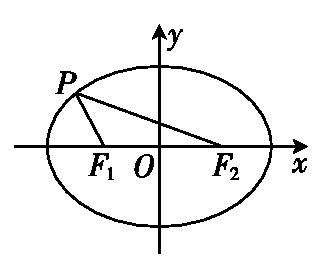

若点P是椭圆上第二象限内的点,且∠PF₁F₂=120°,求△PF₁F₂的面积.

【解析】由题意,可知a=2,b=,所以c=1,|F₁F₂|=2c=2.

在△PF₁F₂中,由余弦定理,得|PF₂|²=|PF₁|²+|F₁F₂|²-2|PF₁||F₁F₂|cos 120°, 即|PF₂|²=|PF₁|²+4+2|PF₁|.　①

由椭圆的定义,得|PF₁|+|PF₂|=4, 即|PF₂|=4-|PF₁|.　②,将②代入①,解得|PF₁|=Error: Reference source not found.

∴S_{PF1F2Error: Reference source not found}=Error: Reference source not found|PF₁||F₁F₂|sin120°=Error: Reference source not found×Error: Reference source not found×2×Error: Reference source not found=即△PF₁F₂

的面积是

【评析】充分利用椭圆定义|PF₁|+|PF₂|=4,解得|PF₁|，再利用三角形面积公式快速得解。

【针对练习2】.已知△ABC的顶点B,C在椭圆+y²=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是(　　).

A.2 B.6 C.4 D.12

【解析】设椭圆的另外一个焦点为F,则由椭圆的定义,知△ABC的周长是|AB|+|BC|+|CA|=|AB|+|BF|+|FC|+|CA|=4a=4.【答案】C

【例3】F₁、F₂为椭圆的两个焦点,过F₂的直线交椭圆于P、Q两点,PF₁⊥PQ且|PF₁|=|PQ|,求椭圆的离心率.

【解析】如图所示,设|PF₁|=m,则|PQ|=m,|F₁Q|=Error: Reference source not foundm.

由椭圆的定义得|PF₁|+|PF₂|=|QF₁|+|QF₂|=2a,

所以|PF₁|+|PQ|+|F₁Q|=4a,即(Error: Reference source not found+2)m=4a.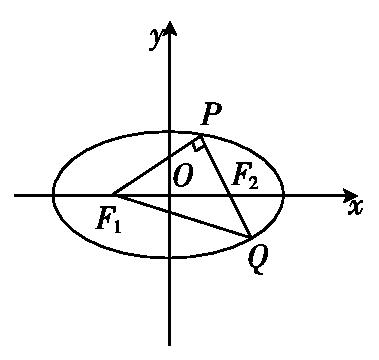

m=(4-2Error: Reference source not found)a.又|PF₂|=2a-m=(2Error: Reference source not found-2)a.

在Rt△PF₁F₂中,|PF₁|²+|PF₂|²=|F₁F₂|²,

即(2Error: Reference source not found-2)²a²+(4-2)²a²=4c².所以Error: Reference source not found=9-6Error: Reference source not found=3(Error: Reference source not found-1)²,所以e==-

【评析】充分利用椭圆定义，根据题中的已知条件化为a、b、c之间的关系,再由离心率定义求出。

【针对练习3】椭圆 的左、右焦点分别为 ，若椭圆上存在一点 使，=则该椭圆的离心率的取值范围为 ；

【解析】在△PF₁F₂中，由正弦定理知=,∵=

∴==, |PF₁|=e|PF₂|①,又点P在椭圆上，∴|PF₁|+|PF₂|=2a ②,由①②联解得|PF₂|=∈(a-c,a+c),即a-c＜＜a+c，同除以a得1-e＜＜1+e, ∴Error: Reference source not found-1＜e＜1

离心率的取值范围为（Error: Reference source not found-1，1）

【评析】求椭圆离心率范围，首先考虑焦半径|PF₂|的范围∈(a-c,a+c),再联解求出|PF₂|=，列出不等式a-c＜＜a+c，最后解出e的范围。

三、利用定义求最值问题

圆锥曲线中涉及距离最小值、距离之和最小值、用定义进行转化,即化折线为直线解决最值问题。过程简捷，结果准确，提高了学生运算能力。

【例4】设P是抛物线y²=4x上的一个动点,F为抛物线的焦点.

（1）若点P到直线x=-1的距离为d,点A(-1,1),求|PA|+d的最小值.

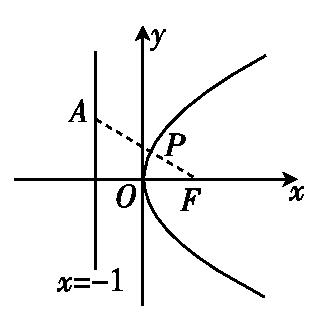
【解析】依题意,抛物线的焦点为F(1,0),准线方程为x=-1.由抛物线的定义,知|PF|=d,于是问题转化为求|PA|+|PF|的最小值.如图,连接AF,交抛物线于点P,则最小值为Error: Reference source not found.

（2）若B(3,2),求|PB|+|PF|的最小值.

【解析】把点B的横坐标代入y²=4x中,得y=±，

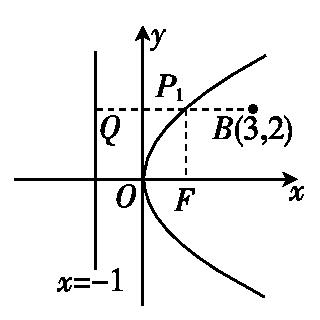
因为Error: Reference source not found>2,所以点B在抛物线内部.过点B作BQ垂直准线于点Q,交抛物线于点P₁(如图).

由抛物线的定义,|P₁Q|=|P₁F|,则|PB|+|PF|≥|P₁B|+|P₁Q|=|BQ|=3+1=4. 即|PB|+|PF|的最小值为4.

【评析】在抛物线中求解与焦点有关的两点间距离和的最小值时,用抛物线的定义进行转化,即化折线为直线解决最值问题最简捷.

【针对练习4】已知点P是抛物线y²=4x上一点,设点P到此抛物线准线的距离为d₁,到直线x+2y-12=0的距离为d₂,则d₁+d₂的最小值是( ).

A.5 B.4 C.Error: Reference source not found D. Error: Reference source not found

【解析】抛物线y²=4x的焦点为(1,0),准线为x=-1,如图,过点F作直线x+2y-12=0的垂线,垂足为D, 则FD与抛物线交于一点P

₁,

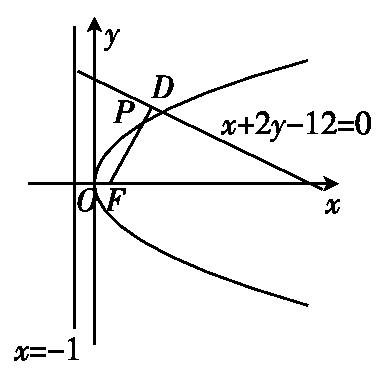
由抛物线定义知，|P₁F|等于点P到此抛物线准线的距离d₁的最小值，|P₁D|=点P到直线x+2y-12=0的距离为d₂最小值，则d₁+d₂的最小值是|DF|=Error: Reference source not found=故选C.【答案】C

【评析】抛物线上的点到其准线的距离等于到其焦点距离是双向的。应用时按需要灵活进行转化达到求解。

实践证明,圆锥曲线的定义是解决解析几何问题的一把钥匙,解析几何中凡是与求轨迹方程，圆锥曲线的焦点、焦半径、离心率,以及求距离最小值、距离之和最小值的问题，活用圆锥曲线定义,常能使解题过程简捷,避免许多复杂的运算.且结果准确，提高了学生的运算能力.

参考文献：

（1）吴彤等.2019 高考“圆锥曲线”专题命题分析[J].中国数学教育，2019（9）：24-27.

（2）喻峥惠等.2019 高考“圆锥曲线”专题解题分析[J].中国数学教育，2019（9）：28-36.

作者信息：张艳春（1963.12）女，汉，山西省五台县人，大学本科，山西省忻州市第一中学数学教师,中小学正高级教师，山西省特级教师，邮编，034000，研究方向，高中数学教育教学。

课题：山西省“十三五”规划课题：提高高中学生几何运算能力的探索与研究----以解析几何为例，课题编号（TJZX--19086）成果之一。

活用定义简化过程提高运算能力 作者：张艳春 Page 4 of 4